ChatGPT - This is pretty awesome :)

[joe.pistell]

anyone using ChatGPT to help with analyzing paid search efforts?

RB, In my AI use (2+ hrs a day in AI), AI doesn't do math well.

 

[Carsten]

chatGPT makes stuff up.

I'm starting to look at just rolling something on my laptop like: WebLLM | Home
There are other models out there.

However, AWS (amazon) just announced they are upgrading their Q and some other things.

I am thinking we are still 1-2 years away from AI that is truly useful.

 

[joe.pistell]

I am thinking we are still 1-2 years away from AI that is truly useful

 

[Rick Buffkin]

Let’s analyze Uncle Joe's AI experience using a formula that quantifies his usage over time and attempt to assess AI’s knowledge of mathematics. Here's how we can approach this:

---

Formula for AI Experience Level​

We define AI Experience Level (E) as a function of time spent daily (T) and total duration in days (D):

E=T⋅DE = T \cdot DE=T⋅D
Where:

• TTT: Time spent daily using AI (in hours, T=2T = 2T=2 for Uncle Joe).
• DDD: Total number of days of usage over the past 6 months (D=6⋅30=180D = 6 \cdot 30 = 180D=6⋅30=180 days).

Formula for AI Knowledge Level at Math​

For simplicity, we assume a relative score, KKK, reflecting AI’s perceived knowledge level in mathematics. This could range from 1 to 100, representing Uncle Joe's subjective rating over time. Let’s hypothesize KKK as proportional to cumulative AI usage experience (E), but capped at a maximum level, Kmax=100K_{\text{max}} = 100Kmax=100:

K=min⁡(Kmax,α⋅E)K = \min(K_{\text{max}}, \alpha \cdot E)K=min(Kmax,α⋅E)
Where:

• Kmax=100K_{\text{max}} = 100Kmax=100: Max score for AI's math knowledge.
• α\alphaα: Scaling factor (α=0.01\alpha = 0.01α=0.01 to keep KKK realistic).

---

Graph Representation​

We’ll graph:

1. Experience Level (E) over 6 months (days: 1 to 180).
2. Knowledge Level (K) over the same period.

Let me compute and plot this.



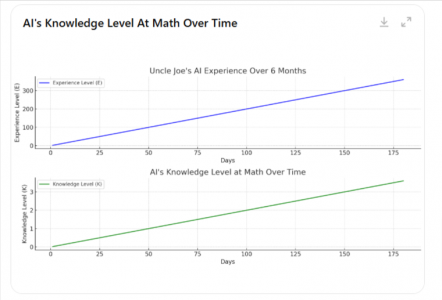
The graphs above represent:

1. Uncle Joe's AI Experience Level (E): This increases linearly over time because he spends a constant amount of 2 hours daily using AI.
2. AI's Knowledge Level at Math (K): This starts growing proportionally with the experience level but caps at a maximum level of 100 due to the imposed limit on AI's perceived maximum capability.

Insights:​

• Uncle Joe's experience grows unbounded as long as he continues using AI.
• The perceived knowledge level of AI in math saturates at a certain point, reflecting the hypothesis of diminishing returns with extended use.

If you'd like to explore further adjustments to this model or focus on a specific scenario, let me know! Keep up the curiosity!